The moving contact line and the nature of the fluid-solid boundary condition

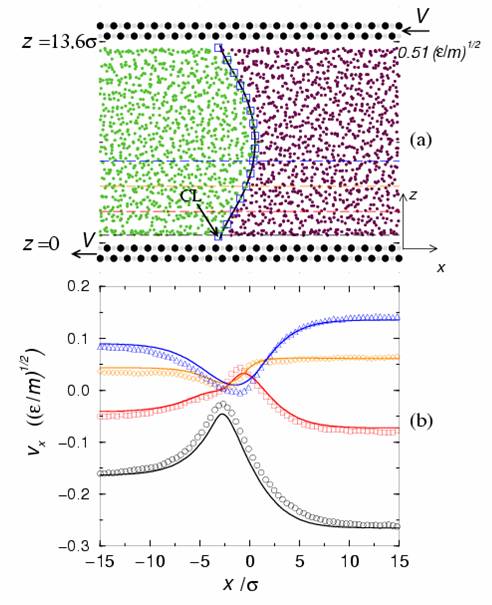
The contact line (CL) denotes the intersection of two immiscible fluid-fluid interface (such as the oil-water interface) with the solid wall, and moving CL arises when one immiscible fluid displaces the other in motion.  The moving CL has been a classical problem in hydrodynamics because it is incompatible with the non-slip boundary condition (yielding infinite dissipation). This is in spite of the fact that the non-slip boundary condition represents one of two pillars (the other being the Navier-Stokes equation) of classical hydrodynamics. While molecular dynamics (MD) simulations have clearly shown nearly total slip of the moving CL (i.e., relative motion with respect to the solid wall), no continuum boundary condition was ever found which can reproduce the MD results, leading to some proposal that hydrodynamics breaks down in the vicinity of the moving CL.  The inability of continuum hydrodynamics to calculate the behavior of the moving CL means accurate nanofluidics or microfluidics simulations would not be possible.  We have successfully resolved this classical problem, with the discovery of the Generalized Navier Boundary Condition (GNBC) for the moving contact line (CL) problem [1,2] and the formulation of a continuum hydrodynamics which yields predictions in quantitative agreement with those from the MD.  A surprising implication of this discovery is that partial slipping can occur at even low shear rates, and the transition of total slipping at the moving CL to non-slipping far away is represented by a power law, where x represents the distance away from the moving CL.

 

Representative publications

1. “Power-law slip profile of the moving contact line in two-phase immiscible flows,” T. Qian, X. P. Wang and Ping Sheng, Phys. Rev. Lett. 93, 094501-094504 (2004).
2. “Molecular scale contact line hydrodynamics of immiscible flows,” T. Qian, X. P. Wang and Ping Sheng, Phys. Rev. E 68, 016306 (2003).