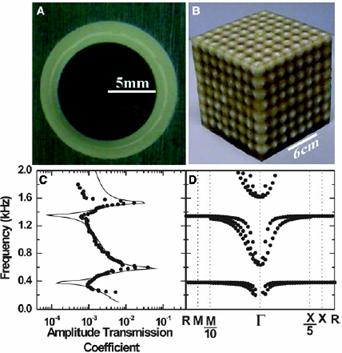
Locally Resonant Sonic Material (LRSM) is designed to reject sound waves at a pre-specified range of frequencies by local resonance. The physical origin of perfect reflection of sound wave in LRSM is very different from conventional phononic crystals (or sonic crystals). Conventional phononic crystals operate under the principle of Bragg reflection, which dictates that the thickness of the slab must be a few times the wavelength of sound. This makes Bragg-reflection based band gap material too bulky for low frequency applications since low frequency sound has a long wavelength. Our material, on the other hand, has sonic band gaps by virtue of arrays of local resonators (see Fig. 1 (B) for the LRSM of the first generation). There are several advantages of using LRSMs to reject sound. Firstly, periodicity is not required (in contrast to Bragg reflection). Secondly, the resonance frequency has nothing to do with the lattice constant, and hence the slab can in principle be much thinner than the wavelength of the sound it is supposed to shield.
For the first generation LRSM, each resonant unit (see Fig. 1 (A)) has a low frequency resonance at 400 Hertz plus some higher frequency resonances. When the resonant units are assembled together in the form of a sonic crystal (e.g. simple cubic structure in Fig. 1 (B)), the sonic transmission exhibits a sonic gap at 400 Hertz. This is verified experimentally and computationally (Fig. 1 (C) and (D)). It can be understood by using a very simple mechanical model.
The result is remarkable, since the wavelength of a 400 Hertz sound wave in the matrix material is about 300 times the lattice constant. Thus away from the resonance, the material can be homogenized, and the elastic waves do not “see” the structural units. However, close to the resonances, the large dispersion of the response function (similar to a very large index of refraction for light) means that the effective wavelength is much smaller and becomes comparable to the lattice constant, hence causing a strong scattering. This peculiar material can break the so-called “mass law” of sound transmission.
Key publication:
- “Locally Resonant Sonic Materials”, Zhengyou Liu, Xixiang Zhang, Yiwei Mao, Y. Y. Zhu, Zhiyu Yang, C. T. Chan, and Ping Sheng, Science, Sep 8 2000: 1734-1736.