The no-slip boundary condition (NSBC) states that there is no relative motion at the fluid-solid interface. It is one of the two pillars in hydrodynamics (the other one being the Navier-Stokes equation). Over the years, NSBC has demonstrated broad applicability, in spite of the fact that there has been no first-principles justification. However, starting about fifty years ago there has been a particularly persistent problem associated with the application of NSBC to the moving contact line in two-phase immiscible flows. The contact line is defined to be the intersection of the fluid-fluid interface with the solid wall. In 1974, it was shown by Dussan and Davis that the application of NSBC leads to a stress singularity for the moving contact line (MCL) problem. This was followed by molecular dynamic (MD) simulations in 1988 showing total slip, not no-slip, for the MCL. And away from the MCL MD simulations have also shown partial slip in the single-phase flow regime. Thus the MCL problem means that the usual continuum hydrodynamics can not accurately model fluids flow on the micro/nano scale. This was sometimes referred to as an example of the “breakdown of continuum.”
Author: PingSheng
Ultrasound tunneling and focusing through phononic crystals
Tunneling is usually regarded as a quantum mechanical phenomenon. However, more generally it is also a wave phenomenon. In collaboration with Prof. John Page of the University of Manitoba, we have observed tunneling by ultrasound through a phononic crystal made of 0.8 mm diameter tungsten carbide beads, immersed in water. The tunneling phenomenon is characterized by a constant pulse traversing time through the phononic crystal sample, independent of the sample thickness. Therefore one can obtain fairly large group velocities for thick samples, although in such cases the signal amplitude is small. Compared with photon tunneling through photonic crystals, we found the tunnling time to be much larger. In fact, the tunneling time is roughly inversely proportional to the gap width. Thus the much higher frequency photonic bandgap implies a much shorter tunneling time.
Continue reading Ultrasound tunneling and focusing through phononic crystals
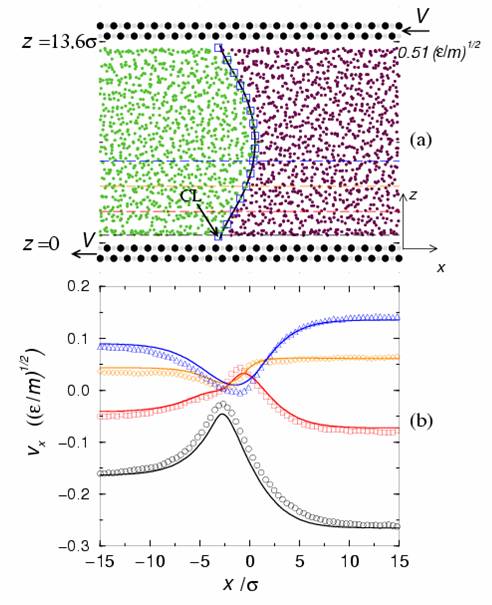
The moving contact line and the nature of the fluid-solid boundary condition
The contact line (CL) denotes the intersection of two immiscible fluid-fluid interface (such as the oil-water interface) with the solid wall, and moving CL arises when one immiscible fluid displaces the other in motion. The moving CL has been a classical problem in hydrodynamics because it is incompatible with the non-slip boundary condition (yielding infinite dissipation). This is in spite of the fact that the non-slip boundary condition represents one of two pillars (the other being the Navier-Stokes equation) of classical hydrodynamics. While molecular dynamics (MD) simulations have clearly shown nearly total slip of the moving CL (i.e., relative motion with respect to the solid wall), no continuum boundary condition was ever found which can reproduce the MD results, leading to some proposal that hydrodynamics breaks down in the vicinity of the moving CL. The inability of continuum hydrodynamics to calculate the behavior of the moving CL means accurate nanofluidics or microfluidics simulations would not be possible. We have successfully resolved this classical problem, with the discovery of the Generalized Navier Boundary Condition (GNBC) for the moving contact line (CL) problem [1,2] and the formulation of a continuum hydrodynamics which yields predictions in quantitative agreement with those from the MD. A surprising implication of this discovery is that partial slipping can occur at even low shear rates, and the transition of total slipping at the moving CL to non-slipping far away is represented by a ![]() power law, where x represents the distance away from the moving CL.
power law, where x represents the distance away from the moving CL.
Representative publications
- “Power-law slip profile of the moving contact line in two-phase immiscible flows,” T. Qian, X. P. Wang and Ping Sheng, Phys. Rev. Lett. 93, 094501-094504 (2004).
- “Molecular scale contact line hydrodynamics of immiscible flows,” T. Qian, X. P. Wang and Ping Sheng, Phys. Rev. E 68, 016306 (2003).
Electrorheological fluids
Eectrorheology denotes the control of a material’s flow properties (rheology) through the application of an electric field. ER fluid was discovered sixty years ago. In the early days the ER fluids, generally consisting of solid particles suspended in an electrically insulating oil, exhibited only a limited range of viscosity change under an electric field, typically in the range of 1-3 kV/mm. The study of ER fluid was revived in the 1980’s, propelled by the envisioned potential applications, as well as the successful fabrication of new ER solid particles that, when suspended in a suitable fluid, can “solidify” under an electric field, with the strength of the high-field solid state characterized by a yield stress (breaking stress under shear). However, further progress was hindered by the barrier of low yield stress (typically in the range of a few kPa).
Liquid crystal-substrate interaction
Alignment of liquid crystal’s orientational order, through its interaction with the substrate, is a critical element in liquid crystal (LC) displays. As an extension of the pioneering study on such interactions [1,2], the recent research focus on this topic is on the use of micro / nanotextured substrates for producing uniform alignment of nematic LC’s orientational ordering [3,4]. The basic principle underlying this approach is “frustration,” i.e., when the elastic energy required for the boundary LC layer to following the micro / nanotextured pattern exceeds a certain threshold, it becomes energetically favorable to sacrifice the interfacial interaction energy so as to minimize the elastic energy, by making a transition to a uniform alignment. What we have found is that by using such micro / nanotextured substrates, one can achieve large pretilt angles, e.g., on the order of 40 degrees (between the symmetry axis of the nematic LC and the substrate). This has been experimentally verified [3]. Large pretilt angles are useful for making bistable LC displays, with the advantage of energy savings.

Representative publications:
- “Phase Transition in Surface-Aligned Nematic Films,” P. Sheng, Phys. Rev. Lett. 37, 1059 (1976).
- “Boundary-layer phase transition in nematic liquid crystals,” P. Sheng, Phys. Rev. A26, 1610 (1982).
- “Liquid crystal orientation transition on microtextured substrates,” B. S. Zhang, F. K. Lee, O. K. C. Tsui and P. Sheng, Phys. Rev. Lett. 91, 215501 (2003).
- “Liquid-crystal phase transitions induced by microtextured substrates,” T. Z. Qian and P. Sheng, Phys. Rev. Lett. 77, 4564 (1996).