Category: Research Highlights

Liquid crystals

  • Pioneered in the study of substrate-induced phenomena in nematic liquid crystals, with predictions verified by subsequent experiments.

Alignment of liquid crystal’s orientational order, through its interaction with the substrate, is a critical element in liquid crystal (LC) displays.  As an extension of the pioneering study on such interactions [1,2], the recent research focus on this topic is on the use of micro / nanotextured substrates for producing uniform alignment of nematic LC’s orientational ordering [3,4].  The basic principle underlying this approach is “frustration,” i.e., when the elastic energy required for the boundary LC layer to following the micro / nanotextured pattern exceeds a certain threshold, it becomes energetically favorable to sacrifice the interfacial interaction energy so as to minimize the elastic energy, by making a transition to a uniform alignment.  What we have found is that by using such micro / nanotextured substrates, one can achieve large pretilt angles, e.g., on the order of 40 degrees (between the symmetry axis of the nematic LC and the substrate).  This has been experimentally verified [4].  Large pretilt angles are useful for making bistable LC displays, with the advantage of energy savings.

Continue reading Liquid crystals

Generic wave characteristics in heterogeneous materials

  • Formulated a theoretical framework for the quantitative prediction of wave phenomena in the intermediate frequency regime. The theory resolves the classical problem concerning the definition and calculation of group velocity in a strongly scattering medium, and gives quantitative explanation of observed multiple acoustic modes in colloidal systems.

Continue reading Generic wave characteristics in heterogeneous materials

Electro-and magnetorheological fluids

Electrorheology denotes the control of a material’s flow properties (rheology) through the application of an electric field.  ER fluid was discovered sixty years ago.  In the early days the ER fluids, generally consisting of solid particles suspended in an electrically insulating oil, exhibited only a limited range of viscosity change under an electric field, typically in the range of 1-3 kV/mm.  The study of ER fluid was revived in the 1980’s, propelled by the envisioned potential applications, as well as the successful fabrication of new ER solid particles that, when suspended in a suitable fluid, can “solidify” under an electric field, with the strength of the high-field solid state characterized by a yield stress (breaking stress under shear).  However, further progress was hindered by the barrier of low yield stress (typically in the range of a few kPa). Continue reading Electro-and magnetorheological fluids

Negative dynamic mass density and locally resonant sonic materials

Negative dynamic mass density for composites

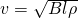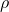Mass density of a composite D is generally regarded as the volume average of its components’densities and hence must be positive. One application of the mass density is in predicting the wave velocity: v = \sqrt{B l \rho}  , where  v  is the longitudinal wave velocity, B the bulk modulus, and  \rho  the dynamic mass density. The question is: Does 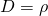D = \rho  necessarily for all composites? We have shown through rigorous derivation with experimental support that the correct answer to the above question is “No.” Moreover,  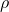\rho  can be negative when there is a resonance in the 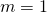m = 1 angular channel of wave scattering. What that implies is that there can indeed be a one-to-one correspondence between the electromagnetic metamaterials, in which both the electric and magnetic permeabilities are negative, and the acoustic metamaterials, in which both the dynamic mass density and bulk modulus are negative. In fact, the negative dynamic mass density was realized through the locally resonant sonic materials, shown below.

 

Key publications:

  1. “Effective Dynamic Mass Density of Composites“, J. Mei, Z. Liu, W. Wen and Ping Sheng, Phys. Rev. B 76, 134205 (2007).
  2. “Dynamic Mass Density and Acoustic Metamaterials“, J. Mei, Z. Liu, W. Wen and Ping Sheng, Physica B 394, 256-261 (2007).
  3. “Effective Mass Density of Fluid-Solid Composites“, J. Mei, Z. Liu, W. Wen and Ping Sheng, Phys. Rev. Lett. 97, 044501 (2006).
  4. “Analytic Model of Phononic Crystals with Local Resonances“, Z. Liu, C. T. Chan and Ping Sheng, Phys. Rev. B71, 014103 (2005).

 

Locally resonant sonic materials

The locally resonant sonic material is designed to reject completely sound waves at a pre- specified range of frequencies. The perfect reflection is achieved by creating elastic wave band gaps induced by local resonances. Conventional elastic wave band gap material operates under the principle of Bragg reflection, which dictates that the thickness of the slab must be a few times of the sound wave to shield. This makes Bragg-reflection based band gap material too bulky for low frequency applications since low frequency sound has long wavelength. Our material has sonic band gaps by virtue of the vibrational resonance of certain structural unit(s). There are several advantages of using resonance to create a band gap. First, periodicity is not required (in contrast to Bragg reflection). Second, the resonance frequency has nothing to do with the lattice constant, and hence the slab can in principle be much thinner than the wavelength of the sound it is supposed to shield.

This unit has a low frequency resonance, at 400 Hertz, plus a higher frequency resonance. When assembled together in the form of a simple cubic sonic crystal, the measured sonic transmission exhibits a sonic gap at 400 Hertz. This is remarkable, since the wavelength of 400 Hertz sound wave in the matrix material is about 300 times the lattice constant. Thus away from the resonance, the material can be homogenized, and the elastic waves do not “see” the structural units. However, close to the resonances, the large dispersion of the response function (similar to a very large index of refraction for light) means that the effective wavelength is much smaller and becomes comparable to the lattice constant, hence the strong scattering. This peculiar material can break the so-called “mass law” of sound transmission. It should be noted that an attenuation gap can be due either to negative elastic constant or to negative dynamic mass density. In the publication below, the effect was wrongly attributed to negative elastic constant, but this has been corrected in the subsequent publications (see above).

 

Key publication:

  1. “Locally Resonant Sonic Materials“, Zhengyou Liu, Xixiang Zhang, Yiwei Mao, Y. Y. Zhu, Zhiyu Yang, C. T. Chan, and Ping Sheng, Science 289, 1734-1736.