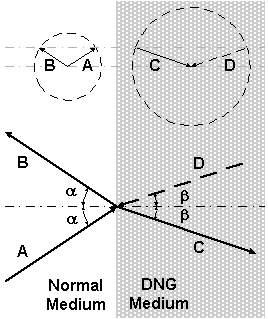
Double negativity in acoustic waves – Prof. Ping Sheng, Physics Department, HKUST

It has been demonstrated that light bends into the “wrong” quadrant when impinging from a normal medium to a double negative (DNG) medium. A DNG medium in electromagnetism is regarded as an effectively homogeneous medium having both negative permittivity and negative permeability. Here, we prove that such a concept can apply also to other kinds of classical waves. In particular, for acoustic waves, if we want sound to bend into the “wrong” quadrant after hitting an interface between air and the DNG medium, it turns out that we need a double negativity in both density and bulk modulus for the DNG medium.

Physically, this means that the medium displays anomalous response at some frequencies such that it expands upon compression (negative bulk modulus) and moves to the left when being pushed to the right (negative density) at the same time. However, all natural materials have positive density and positive bulk modulus only! It sounds strange, right?

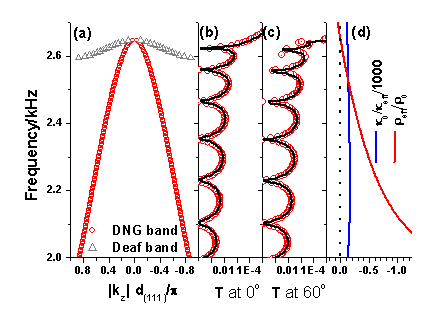
Figure 1: Ray diagram for a wave incident from a normal to a DNG medium: (A) incident beam; (B) reflected beam; (C) the refracted beam in the “wrong” quadrant; (D) the original refracted beam if the DNG medium is replaced by a normal medium.

A detailed analysis shows that it is possible in principle to achieve double negativity in acoustic waves if resonance structures are employed in the material. As an example, for a composite with soft rubber spheres dispersed in water, there is a frequency regime in which the effective density ( $\rho_{eff}$ ) and the effective bulk modulus ( $\kappa_{eff}$ ) are both negative. The usefulness of assigning negative density and negative bulk modulus to the medium is demonstrated by calculating the transmittance through a finite slab of the composite at various incidence angles. There is no significant difference in results calculated by a multiple-scattering approach which takes care of the microstructure of the composite and by simple formulas which assume that the slab is a homogeneous medium of effective density and bulk modulus. In this particular case, the resonance is driven by the high contrast in sound speed between the rubber and water. A mono-polar resonance for the rubber sphere gives rise to negative bulk modulus while a dipolar resonance for the rubber sphere gives rise to negative density. The mono-polar resonance in this case is broad enough to cover the frequency regime of dipolar resonance as well, so that we can have only one resonance structure instead of two to obtain double negativity. This work has been published in Phys. Rev. E 70, 055602(R).