Evanescent waves can play an important role in meta-materials. The most famous example is the Perfect Lens invented by J B Pendry. The lens, a flat slab of material with both permittivity and permeability being minus one, can attain a sub-wavelength resolution by amplifying the evanescent wave within the lens. However, for evanescent waves with bigger and bigger transverse wave vectors, it is expected that the microstructure starts to become important so that the physics deviates from the local effective medium description of the meta-material.
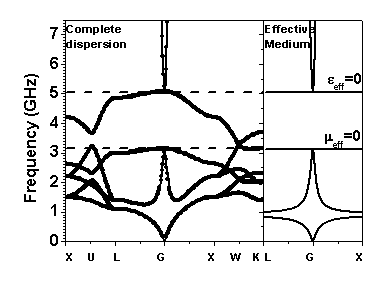
In order to investigate the effect of microstructure, a dipolar model is employed to model the metamaterial so that on one hand we can derive the local effective medium directly. On the other hand, a complete (
, 
) dispersion diagram can be obtained with microstructure taken into consideration. As a result, the complete dispersion diagram converges to the local effective medium description only near the Brillouin zone center.
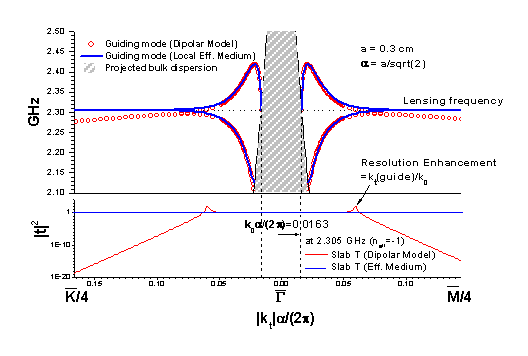
The same model has been applied to the perfect lens. To be more specific, we calculate the guiding mode dispersion of the perfect lens. Under the local effective medium description, the dispersion never crosses with the lensing frequency and the transmission amplitude always stay at a constant one at different transverse wave vectors. This signifies a perfect resolution. However, under the dipolar model, the dispersion crosses with the lensing frequency with a very small transverse wave vector. We found that this effect on the resolution dominates over other effects like impedance mismatch and absorption, which decreases the resolution. From this model, we can discuss the situation exactly at the perfect lens condition without field divergence. Moreover, the resolution enhancement of the perfect lens is still a near-field effect under the dipolar model. The resolution converges to the one corresponding to the traditional diffraction limit if we increase the thickness of the lens.
